Dimensionamento Estrutural
Este artefato aborda o desenvolvimento das principais análises necessárias para garantir a funcionalidade, segurança e eficiência da cadeira de rodas projetada. Foram detalhadas quatro áreas principais: o cálculo do torque necessário para o motor impulsionar a cadeira, confirmando que o motor selecionado atende às necessidades de movimento; o dimensionamento do mecanismo de ajuste do apoio de pernas, do apoio de cabeça e da rodinha anti-tombamento.
Inicialmente, o torque necessário foi analisado com base no balanço de forças para superar o caso estático do movimento, considerando as forças atuantes no sistema em uma rampa inclinada. Para garantir precisão e confiabilidade nos cálculos, os dados de entrada utilizados foram definidos com base em normas regulamentadoras, assegurando conformidade com os requisitos técnicos e de segurança.
Em seguida, o foco foi o dimensionamento e os cálculos estruturais para o mecanismo de ajuste do apoio de pernas. Os cálculos englobam a análise de forças, momentos e tensões. Foram avaliadas as margens de segurança e dimensionados os pinos, garantindo que o mecanismo suporte as cargas aplicadas e funcione de maneira eficiente. Também foi definida a distância entre cada dente da trava para assegurar que a angulação necessária seja provida.
Posteriormente, foi desenvolvido o apoio de cabeça, com regulagens de altura e profundidade, permitindo ajustes para frente e para trás. Este sistema foi projetado para atender às diferentes necessidades dos usuários, oferecendo maior conforto e suporte, especialmente para aqueles que necessitam de estabilidade adicional na região cervical. As análises e dimensionamentos realizados garantem que o mecanismo do apoio de cabeça seja seguro, robusto e de fácil utilização.
Por fim, foram realizados os cálculos para a rodinha anti-tombamento, que visa criar um suporte que entra em contato com o solo no momento exato em que o centro de massa da cadeira ultrapassa o eixo da roda traseira, caracterizando o ponto crítico de instabilidade. O ângulo crítico de tombamento e os comprimentos necessários para garantir o funcionamento do sistema foram definidos.
Assim, este artefato combina fundamentos teóricos e aplicações práticas, resultando em um projeto bem estruturado e tecnicamente fundamentado para a cadeira de rodas.
Normas e referências utilizadas para definição dos dados usados nos cálculos
Cálculo do torque do motor
Para determinar o torque requerido pelo motor da cadeira de rodas motorizada, foi necessário utilizar normas técnicas que definem os parâmetros de entrada no cálculo, garantindo conformidade com requisitos de segurança e funcionalidade.
-
Peso máximo do usuário
Referência: NBR ISO 7176-7:2008 - Cadeiras de Rodas - Parte 7: Medição de dimensões de assentos e rodas
Aplicação: O peso máximo seguro recomendado por esta norma é de até 120 kg. Este valor foi confirmado pelo fabricante da cadeira de rodas original da Ortobras e foi utilizado nos cálculos para representar a carga máxima suportada.
-
Coeficiente de atrito estático
Referência: NBR ISO 7176-13:2009 - Determinação do coeficiente de atrito de superficies de ensaio; Livro: Estática: Mecanica para Engenharia" de Hibbeler.
Aplicação: De acordo com a NBR 7176-13, o coeficiente de atrito estático entre borracha e cerâmica varia entre 0,75 e 1,00. Para esta análise, foi adotado o valor de 0,85, um valor médio conforme o livro "Estática: Mecânica para Engenharia" de Hibbeler.
-
Inclinação usada nos cálculos
Referência: NBR ISO 7176-3/2015: Cadeiras de Rodas - Determinação da Eficácia dos Freios
Aplicação: Recomenda-se inclinações de até 10° para cálculos e testes, conforme a norma.
Dimensionamento do mecanismo móvel para apoio de pernas
O dimensionamento do mecanismo de apoio de pernas incluiu a análise de forças e momentos aplicados durante o uso em diferentes posições. Para garantir que as inclinações do apoio atendam aos requisitos ergonômicos e de segurança, foram consideradas as seguintes referências:
-
Ângulo de inclinação
Referência: NBR ISO 7176-7: Cadeiras de rodas – Parte 7: Medição das dimensões, massa e desempenho
Aplicação: A definifição do ângulo de inclinação foi avaliado conforme definido pela norma, considerando os eixos de referência entre o plano das pernas e a superfície do assento.
-
Massa do segmento corporal
Referência: NBR ISO 7176-11: Cadeiras de rodas – Parte 11: Bonecos de Ensaio
Aplicação: Para a determinação da massa das pernas proporcional ao peso corporal, adotou-se que, para usuários com peso igual ou superior a 100 kg, a massa do segmento da perna deve ser considerada como 9 kg, conforme consta na norma.
-
Propriedades dos parafusos
Referência: ISO 898-1: Mechanical properties of fasteners made of carbon steel and alloy steel – Part 1: Bolts, screws and studs
Aplicação: A área de seção nominal do parafuso foi definida como 36,61 mm², conforme especificado na norma para parafusos de classe M8. Além disso, a norma foi utilizada para a análise das resistências mecânicas, a fim de selecionar adequadamente a classe de aço mais apropriada para a aplicação.
Dimensionamento do apoio regulável de cabeça
-
Dimensões antropométricas
Referência: NBR ISO 7176-7: Cadeiras de rodas – Parte 7: Medição de dimensões de assentos e rodas
Aplicação: Foram determinadas as distâncias corporais de referência para aplicação no software Catia.
Dimensionamento dos dispositivos antitombo traseiros
-
Definição Conceitual do Esquema de Forças
Referência: NBR ISO 7176-1: Cadeiras de Rodas - Parte 1: Determinação da Estabilidade Estática
Aplicação: A norma fornece os procedimentos para a avaliação da estabilidade da cadeira de rodas em diferentes direções, incluindo a traseira. Embora a norma não especifique exatamente quais devem ser os ângulos do dispositivo antitombo, ela define a logica para determinar o ângulo de tombamento crítico e os critérios para considerar uma cadeira estável.
Cálculo do torque requerido do motor para a cadeira de rodas
Para determinar o torque necessário ao motor que impulsiona a cadeira de rodas, foi realizada uma análise detalhada, considerando que um motor pré-selecionado, de fácil acesso e viabilidade financeira, seria utilizado. O objetivo da análise foi verificar se este motor seria capaz de atender às demandas do sistema. A condição mais crítica foi analisada: o movimento em um plano inclinado, com o cálculo do torque necessário para superar a condição de equilíbrio. Assim, qualquer torque superior a esse valor garantiria que a cadeira de rodas se movimentasse. Essa abordagem foi adotada devido à ausência de dados normativos específicos sobre a aceleração da cadeira, concentrando-se na condição mínima necessária para o funcionamento.
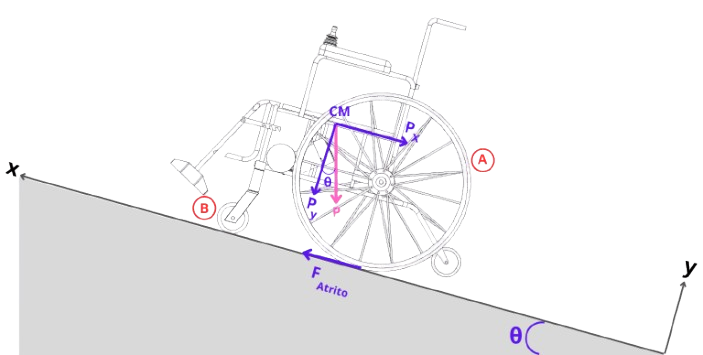
A condição analisada está ilustrada na Imagem 1, representando o cenário avaliado no estudo.
Parâmetros de entrada
Os cálculos foram realizados com base nos seguintes parâmetros, com as referencias ja mencionadas anteriormente.
- Massa do usuário (mu): 120 kg - Representa o peso médio padronizado suportado pela cadeira de rodas.
- Massa da cadeira (mc): 25,65 kg - Inclui a estrutura metálica, os sistemas de roda e o mecanismo de suporte, além da eletrônica e dispositivos de energia.
- Raio da roda principal (Ra): 0,3 m.
- Raio da roda de fricção (Rfric): 0,0485 m.
- Aceleração gravitacional (g): 9,81 m/s².
- Angulo de inclinação da rampa (teta): 10°
- Coeficiente de atrito entre a borracha e a ceramica (u): 0,85
- Distancia horizontal da roda A ate o cm (a):0,151656m
- Distancia horizontal da roda B ate o cm (b):0,302546m
- Distancia vertical da roda A ate o cm (d):0,256757m
- Distancia vertical da roda B ate o cm (c):0,508872m
Etapas do cálculo
Passo 1: Cálculo do peso total e projeções
O valor total da massa foi inicialmente estimado como a soma da massa do usuário e da cadeira, incluindo seus componentes e dispositivos. O peso total da cadeira de rodas, considerando tanto a estrutura quanto o peso do usuário e dos dispositivos, foi calculado multiplicando a massa total pela aceleração gravitacional. Em seguida, o peso foi decomposto nas componentes dos eixos horizontal (x) e vertical (y), levando em consideração a inclinação da rampa, que representa o cenário mais crítico.
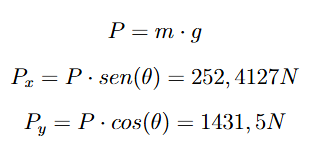
Considerando a decomposição da força peso, é possível realizar a análise do balanço de forças nos eixos de referência, incluindo todas as forças envolvidas. Esse balanço, que leva em conta a condição de equilíbrio necessária para superar a rampa, está ilustrado na Imagem 2, abaixo.
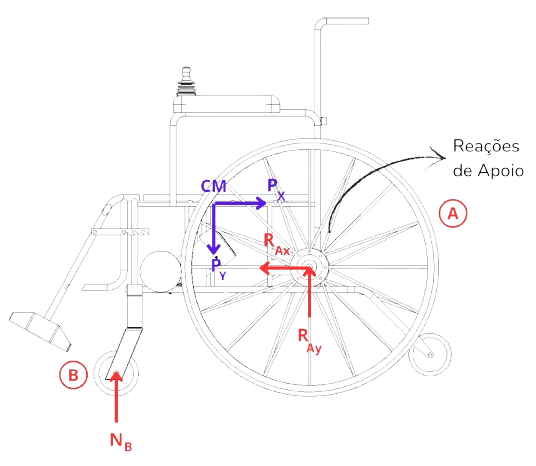
Com esses valores já decompostos, os próximos passos envolvem o cálculo das reações de apoio na roda A, representadas por RAy e RAx.
Passo 2: Balanço de forças no eixo vertical
O próximo passo do cálculo foi estabelecer uma relação que permitisse determinar o parâmetro RAy. Para isso, foi realizado o somatório das forças no eixo y. As reações normais das rodas dianteira e traseira foram somadas e igualadas à componente do peso projetada na direção y. Esse procedimento resultou em uma expressão que viabiliza o cálculo de RAy.
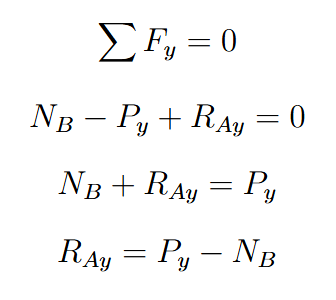
Passo 3: Balanço de momentos na roda A
Para determinar o valor de NB, foi realizado o somatório dos momentos em torno do ponto de apoio da roda A. As forças significativas para esse cálculo foram os momentos gerados por NB, Py e Px, já que as demais forças atuavam diretamente na linha de ação do apoio e, portanto, não possuíam braço de alavanca. Utilizando as distâncias indicadas na Imagem 3, foi possível relacionar essas forças às respectivas alavancas para calcular os momentos.
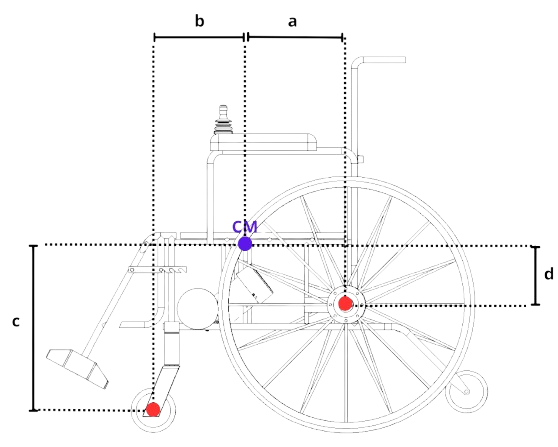
Com isso, o valor de NB pode ser encontrado:
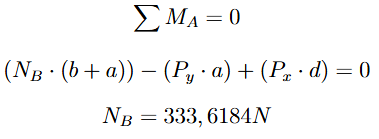
Após determinar o valor de NB, foi possível retornar ao equacionamento inicial para calcular RAy e, assim, obter seu valor.
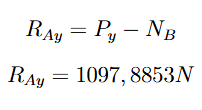
Passo 4: Equilíbrio das forças: somatório igual a zero
Após determinar o valor da reação de apoio em y, o próximo passo é calcular a reação de apoio em x (RAx). Para isso, aplica-se o conceito da segunda lei de Newton, que estabelece que o somatório das forças (força resultante) é igual à massa vezes a aceleração. No entanto, como estamos lidando com a condição de superar o estado inicial de equilíbrio sem considerar aceleração, esse somatório é igual a zero. Esse princípio é aplicado ao eixo horizontal para determinar o valor de RAx.
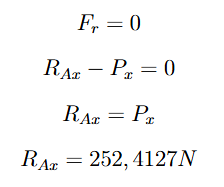
Passo 5: Balanço de forças no eixo vertical na roda A
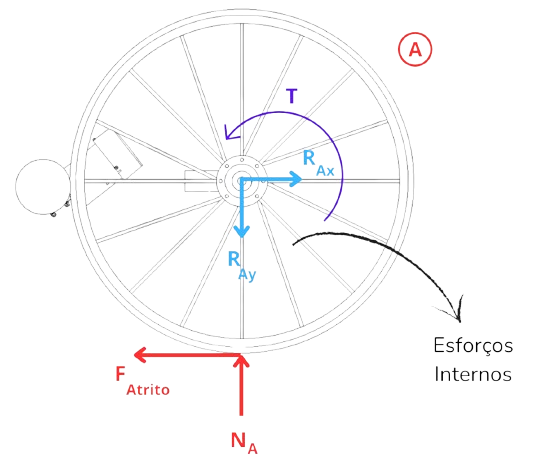
Com os valores das reações de apoio na roda já determinados, podemos interpretá-los como ações externas aplicadas à roda. Para calcular os esforços internos que atuam na roda, consideramos as forças com o mesmo módulo e sinais opostos às reações de apoio, pois os esforços internos equilibram as ações externas. Focando na roda A, obtemos um desenho esquemático detalhado das forças que agem sobre ela, como mostrado na Imagem 4. Em seguida, o somatório das forças no eixo y é igualado a zero para atender à condição de equilíbrio. Esse procedimento permite determinar o valor da força normal que atua na roda A (NA).
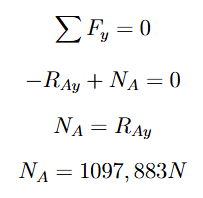
Passo 6: Cálculo da força de atrito
A partir do valor da força normal (NA) calculado, o próximo passo é determinar a força de atrito para, finalmente, calcular o torque na roda A. Para isso, devemos considerar duas forças de atrito: a força de atrito necessária e a força de atrito máxima, de acordo com o livro Estática: Mecânica para Engenharia de Hibbeler.
-
Força de atrito necessária: A força de atrito necessária foi obtida pela segunda lei de Newton, que indica que a força de atrito necessária é igual ao valor de RAx. Isso ocorre porque, no caso de equilíbrio, sem aceleração, a força de atrito necessária precisa balancear a força horizontal de reação RAx, garantindo que a roda não deslize e possa se mover.
-
Força de atrito máxima: A força de atrito máxima é determinada pelo coeficiente de atrito estático multiplicado pela força normal. Essa é a força limite que pode ser gerada pela interação entre a roda e a superfície antes que ocorra o deslizamento.
A força de atrito máxima é a força que garante a condição de não deslizamento da roda. Ou seja, se a força de atrito necessária for menor ou igual à força de atrito máxima, a roda não desliza, e o movimento ocorre de forma eficiente, sem patinar sobre a superfície.

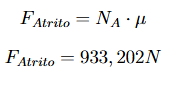
Como a força de atrito necessária é menor que a força de atrito máxima, isso nos dá a certeza de que a roda não irá rodar em falso, ou seja, não ocorrerá deslizamento. Dessa forma, temos a garantia de que a roda vai rodar corretamente, mantendo aderência à superfície. Com isso, podemos prosseguir para o cálculo do torque na roda A, levando em consideração a força de atrito como um dos fatores essenciais para determinar o momento de rotação.
Passo 7: Cálculo do torque na roda
Agora, para o cálculo do torque na roda A, a força de atrito necessária será multiplicada pelo raio da roda A. Essa escolha é feita porque a força de atrito necessária é a que equilibra as forças horizontais sem causar aceleração, sendo a que efetivamente atua para mover a roda.
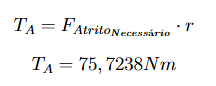
Passo 8: Relação de transmissão
Como o valor do torque calculado anteriormente é considerável, uma roda de fricção é implementada para reduzir o torque diretamente requerido pelo motor. Essa roda funciona como um intermediário, transferindo o torque e ajustando a relação entre as rotações do sistema e do motor. Para calcular o torque transmitido pela roda de fricção, é necessário considerar um fator significativo: a força tangencial no ponto de contato.
Como a força tangencial deve ser a mesma nas duas rodas no ponto de contato, a força de atrito entre as superfícies também deve permanecer constante. Assim, conhecendo os valores do torque na roda A, é possível aplicar uma relação de transmissão para calcular o torque correspondente na roda de fricção. Essa relação é baseada nas proporções dos raios das rodas, conforme descrito no livro Elementos de Máquinas de Shigley. Essa relação pode ser visualizada da seguinte forma:
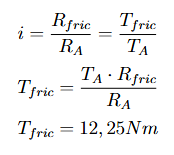
Além disso, é fundamental garantir que o torque seja transmitido sem deslizamento entre as rodas. Para isso, uma premissa básica é que a velocidade periférica de cada roda seja igual no ponto de contato. Com ciência dessa condição, o sistema foi ajustado de forma a eliminar possíveis folgas entre a roda de fricção e a roda de borracha, garantindo o contato firme e contínuo.
Tendo o valor do torque transmitido pela roda de fricção, é importante considerar que o sistema utiliza dois motores para dividir a carga de trabalho. Dessa forma, o torque calculado para a roda de fricção será igualmente distribuído entre os dois motores, ou seja, cada motor será responsável por metade do torque total transmitido.
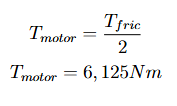
Conclusão
O valor do torque encontrado foi ligeiramente maior do que o motor é capaz de fornecer. Esse resultado acredita-se estar relacionado às condições críticas de análise implementadas durante o projeto, que consideraram cenários de operação mais exigentes do que os normalmente esperados.
Além disso, como o projeto teve como base uma cadeira de rodas proveniente de um desenvolvimento anterior, houve certas limitações em relação à alteração da dinâmica do motor e à implementação da roda de fricção. Essa roda faz parte de uma patente vinculada ao projeto original, o que restringiu a flexibilidade no redesenho.
Dado o contexto, aceitou-se a diferença encontrada no torque, concluindo-se que o projeto apresenta melhor desempenho em condições de uso controladas, como superfícies planas e sem rampas acentuadas. Para atender a essas condições, foi realizado um cálculo iterativo para determinar o ângulo máximo de inclinação suportado pelo torque disponível no motor, resultando em um valor de 4,4°. Esse cenário está alinhado com o escopo original do projeto, pois a cadeira de rodas foi concebida para ser utilizada em ambientes fechados e controlados, como o interior de residências, visto que a integração com a Alexa deve ser um fator mantido.
Mecanismo móvel para apoio de pernas
A ergonomia em cadeiras de rodas é um fator essencial para garantir conforto e segurança aos usuários. Estudos, como o de Carriel e Paschoarelli (2009), ressaltam a importância de componentes como apoios de braços, cabeça e pés na funcionalidade do equipamento, além de identificarem áreas de desconforto associadas à inadequação desses elementos. Nesse contexto, a substituição do apoio de pernas fixo por um sistema ajustável surge como uma solução prática para aprimorar a experiência do usuário, especialmente durante longos períodos de uso.
A manutenção prolongada da postura sentada, sem mudanças frequentes, pode acarretar diversos problemas de saúde, como lesões por pressão e desconfortos musculoesqueléticos, segundo Huet e Moraes (2003). A implementação de um apoio de pernas móvel busca não apenas flexibilizar o posicionamento dos membros inferiores, mas também promover mudanças posturais, reduzindo esses riscos e contribuindo para a qualidade de vida dos usuários.
Neste estudo, são apresentados os cálculos e dimensionamentos necessários para a adaptação do apoio fixo de pernas em um mecanismo móvel. A análise contempla ângulos ajustáveis, forças aplicadas pelos segmentos corporais e os momentos gerados na estrutura, garantindo segurança, funcionalidade e conforto no uso diário da cadeira de rodas.
Definição dos ângulos reguláveis
O ângulo de inclinação foi avaliado conforme as diretrizes estabelecidas na norma ABNT NBR ISO 7176-7, que define os eixos de referência a serem considerados na análise. De acordo com essa norma, a inclinação deve ser mensurada entre o plano das pernas e a superfície do assento, garantindo que o ajuste do apoio de pernas esteja em conformidade com os parâmetros ergonômicos e de segurança exigidos.
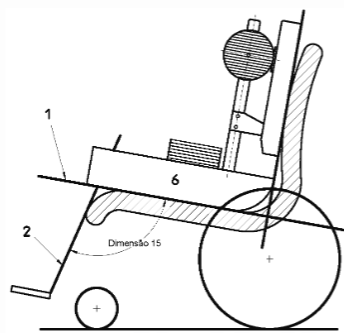
O modelo original da cadeira de rodas, fornecido pela Ortobras, apresenta um ângulo inicial de 120°, considerado uma posição neutra, na qual as pernas permanecem direcionadas para baixo, sem elevação significativa. Com o intuito de aprimorar a ergonomia e o conforto do usuário, foram incorporados dois ângulos adicionais ajustáveis: 140° e 170°.
A inclusão do ângulo de 170° possibilita a extensão quase completa das pernas, o que pode ser benéfico para indivíduos com hipotensão, uma vez que a elevação dos membros inferiores pode contribuir para a melhora da circulação sanguínea e a estabilização da pressão arterial (MSD MANUAL, 2024). Além disso, foi adotado um ângulo intermediário de 140°, representando um incremento de 20° em relação à posição original. Essa escolha fundamenta-se em estudos que apontam que ajustes de inclinação podem melhorar o conforto e a distribuição de pressão para usuários de cadeiras de rodas (BALL, 2017).
- 120º: Posição neutra;
- 140º: Posição intermediária;
- 170°: Posição máxima.
Definição das dimensões da trava e cálculo dos esforços internos
Foram identificados três pontos cruciais para o dimensionamento do sistema:
- Ponto A (Pivô de rotação): Representa o eixo principal que conecta o apoio de pernas à estrutura da cadeira, permitindo a rotação do mecanismo e definindo o movimento do sistema.
- Ponto B (Ponto de fixação da trava): Local onde a trava se prende para garantir que o mecanismo permaneça estável após o ajuste.
- Ponto C (Trava de ajuste): Ponto onde será usinada a peça de trava, sendo responsável por definir as diferentes inclinações do apoio de pernas.

O posicionamento dos pontos A (pivô de rotação) e C (trava de ajuste) foi determinado considerando a estrutura original da cadeira, a fim de garantir a viabilidade da adaptação do sistema. A partir dessas referências, foi calculada a posição do Ponto B e determinadas as distâncias ideais entre os dentes da trava para acomodar cada inclinação, utilizando relações trigonométricas e a lei dos cossenos.
Para avaliar os esforços no sistema, foram calculadas as forças e os momentos para as três configurações de inclinação, considerando os segmentos corporais responsáveis pela carga sobre o apoio: panturrilha e pé. No estudo, adotou-se um peso do usuário de 120 kg, conforme estabelecido anteriormente. A determinação da massa das pernas proporcional ao peso corporal seguiu a norma ABNT NBR 7176-11, que estabelece que, para usuários com peso igual ou superior a 100 kg, a massa do segmento da perna deve ser considerada como 9 kg.
A análise considerou a força peso do segmento e as respectivas linhas de ação nos pontos A, B e C. Os esforços internos em cada ponto foram determinados com base nas equações de equilíbrio estático, que estabelecem que a soma das forças e a soma dos momentos devem ser iguais a zero para um sistema em equilíbrio, conforme apresentado no livro Resistência dos Materiais (BEER et al., 2017). Foram calculados:
- Esforço cortante (V_A) e momento (M) no ponto A;
- Torque (T) gerado nos pontos de trava.
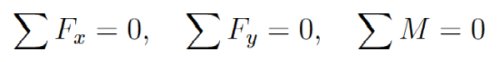
Caso 1: posição neutra
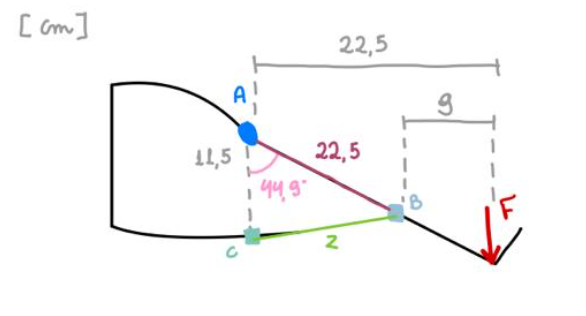
Para o caso 1, foi feito o seguinte esquemático simplificado:
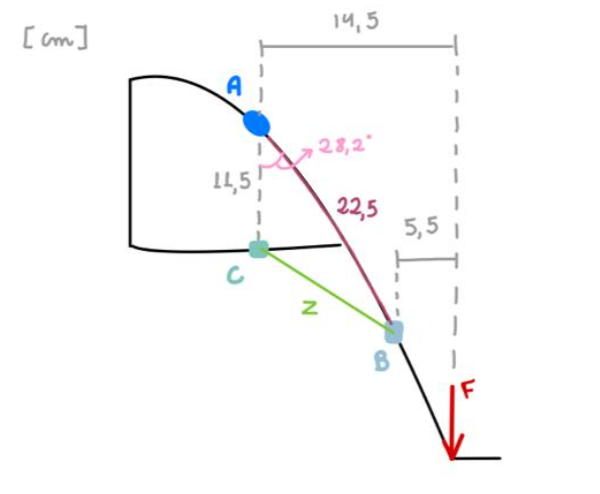
Conforme mencionado anteriormente, os pontos A e C foram posicionados com base na geometria da estrutura e nos elementos pré-existentes da cadeira. A partir dessa definição, foram determinadas as distâncias até o ponto de aplicação da força. Com essas informações, aplicaram-se as equações de equilíbrio estático em cada ponto, resultando em:
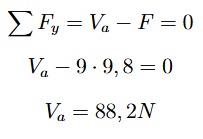
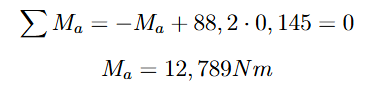
Como os pontos A e C estão a mesma distância horizontal do ponto de aplicação da força:
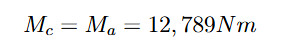
E o torque no ponto B:
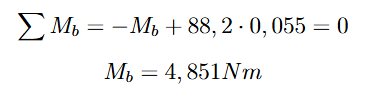
Além da análise dos esforços, é necessário determinar o posicionamento do dente da trava para alcançar a inclinação desejada. Como a geometria envolvida não forma um triângulo retângulo, aplicaremos a Lei dos Cossenos para calcular o valor de z, conforme a equação:
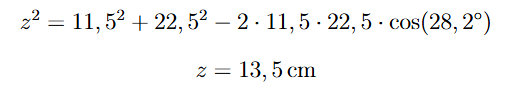
Caso 2: posição intermediária
Como o Ponto B é fixo, é necessário calcular a nova distância entre os Pontos B e C, que corresponde ao tamanho da trava para essa inclinação. Para isso, utilizamos a Lei dos Cossenos novamente, considerando que os pontos A, B e C formam um triângulo, onde o lado BC varia conforme a inclinação desejada.
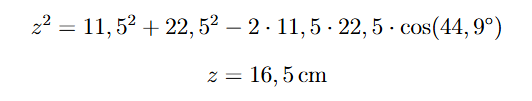
E aplicando o mesmo porcesso para calcular os eforços internos em cada ponto, temos:
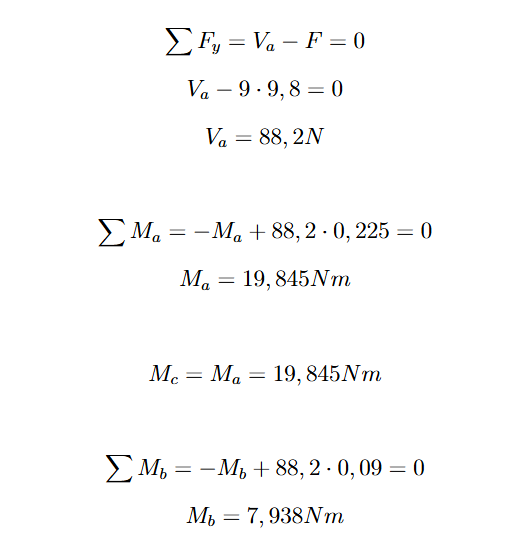
Caso 3: posição máxima
Para o caso da posição máxima:
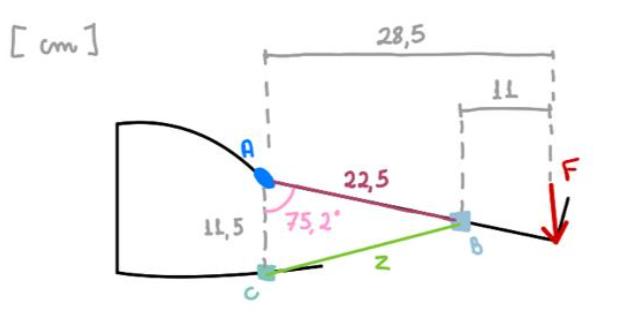
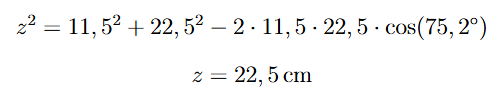
E o esforço cortante e momentos para o caso são:
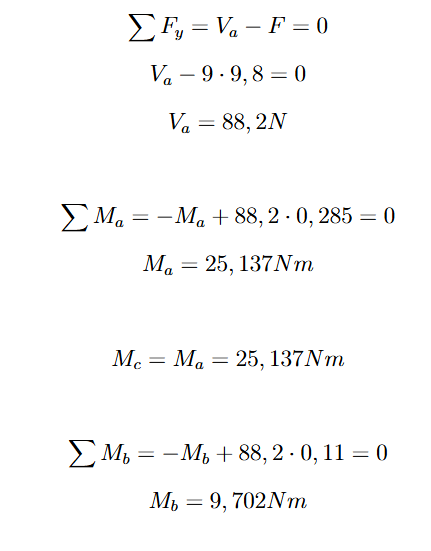
Especificação dos componentes
Dimensionamento dos pinos
Os pinos responsáveis por permitir a rotação e fixação do sistema estarão submetidos a tensões cisalhantes resultantes dos torques transmitidos durante a operação. Para atender às demandas mecânicas previstas, optou-se pela utilização de parafusos métricos padrão M8. Essa escolha se justifica por sua ampla utilização na engenharia mecânica, que proporciona facilidade de substituição, compatibilidade com ferramentas e componentes comerciais, além de garantir elevada confiabilidade estrutural.
O torque gerado no pino pode ser relacionado à força de cisalhamento que atua na seção transversal do pino. A relação entre o torque e a força é dada por:
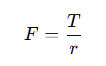
Onde:
- T: torque aplicado;
- F: força de cisalhamento;
- r: raio do pino.
De acordo com a definição, a tensão é a força dividida pela área da seção. No caso de um parafuso M8, embora o diâmetro nominal seja de 8 mm, a área resistente é calculada com base no diâmetro do núcleo do parafuso, e não no diâmetro externo das roscas. Conforme especificado pela norma ISO 898-1, a área resistente de um parafuso M8 é aproximadamente As = 36,6 mm². Dessa forma, a fórmula a ser utilizada para determinar a tensão máxima no parafuso, gerada pelo torque aplicado no sistema, é a seguinte:
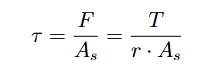
Substituindo os valores em cada ponto foram obtidas as seguintes tensões cisalhantes máximas:
Tabela 1: Tensões cisalhantes máximas aplicadas nos pontos B e C
| Caso | Ponto B [MPa] | Ponto C [Mpa] |
|---|---|---|
| Posição neutra | 33,14 | 87,36 |
| Posição intermediária | 54,22 | 135,55 |
| Posição máxima | 66,27 | 171,17 |
Fonte: Ana Carolina Carvalho
Após calcular a tensão gerada em cada um dos pontos do sistema, é possível selecionar o material a ser utilizado nos apoios. Parafusos estruturais devem ser escolhidos levando-se em conta a resistência de prova do parafuso. As resistências são definida pela classe do parafuso e seu diâmetro nominal, a Tabela 2 mostra as especificações de parafusos segundo a norma ISO.
Tabela 2: Especificações e resistências de parafusos de aço segundo a ISO
| Número de classe | Intervalo de diâmetro externo | Resistência mínima de prova [MPa] | Resistência mínima de escoamento [MPa] | Resistência mínima à tração [MPa] |
|---|---|---|---|---|
| 4.6 | M5-M36 | 225 | 240 | 400 |
| 4.8 | M1,6-M16 | 310 | 340 | 420 |
| 5.8 | M5-M24 | 380 | 420 | 520 |
| 8.8 | M3-M36 | 600 | 660 | 830 |
| 9.8 | M1,6-M16 | 650 | 720 | 900 |
| 10.9 | M5-M36 | 830 | 940 | 1040 |
| 12.9 | M1,6-M36 | 970 | 1100 | 1220 |
Fonte: Norton (2004, p778).
Para determinar a tensão cisalhante que o parafuso pode suportar, adotamos como valor admissível, de acordo com critérios amplamente aceitos na engenharia mecânica, 50% da resistência à tração do material. Essa abordagem conservadora é utilizada no dimensionamento de componentes sujeitos a forças cortantes, garantindo a integridade estrutural em diversas aplicações práticas (NORTON, 2004). Para garantir que o parafuso não entre em regime de deformações plásticas ou falha prematura, utilizaremos 50% da tensão de escoamento como valor para a tensão cisalhante admissível. Com isso, será possível definir as tensões adequadas para cada classe de parafuso, conforme mostrado na Tabela 3.
Tabela 3: Resistência ao cisalhamento em parafusos de aço
| Número de classe | Intervalo de diâmetro externo | Tensão cisalhante admissível [MPa] |
|---|---|---|
| 4.6 | M5-M36 | 120 |
| 4.8 | M1,6-M16 | 170 |
| 5.8 | M5-M24 | 190 |
| 8.8 | M3-M36 | 330 |
| 9.8 | M1,6-M16 | 360 |
| 10.9 | M5-M36 | 470 |
| 12.9 | M1,6-M36 | 610 |
Fonte: Ana Carolina Carvalho
Para a análise de segurança, considerou-se o cenário mais crítico, que ocorre no Ponto C, sob a inclinação máxima. Como todos os outros valores de tensão calculados para os demais pontos estão abaixo desse valor máximo, podemos adotá-lo como referência para a aplicação. Assim, conforme apresentado na Tabela 1, a tensão máxima aplicada é de 171,17 MPa. Para garantir a segurança, é necessário que a tensão admissível (𝜏_adm) seja superior à tensão máxima aplicada (𝜏_max). Com base nisso, podemos descartar os parafusos das classes 4.6 e 4.8, uma vez que, não atendem ao critério de segurança. Além disso, as classes 10.9 e 12.9 podem ser excluídas da análise, pois seu valor de resistência é excessivamente elevado para a aplicação.
Para avaliar a margem de segurança (MS), calculou-se o fator de segurança (FS), que é a razão entre a tensão admissível e a tensão máxima gerada no parafuso:
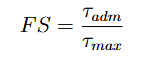
Tabela 4: Fatores de segurança
| Número de classe | Fator de segurança |
|---|---|
| 5.8 | 1,11 |
| 8.8 | 1,93 |
| 9.8 | 2,10 |
Fonte: Ana Carolina Carvalho
A partir do FS calculado, é possível determinar a MS, que é calculada pela diferença entre o FS e 1, multiplicada por 100 para expressá-la em termos percentuais.
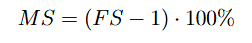
Esse cálculo indica o quanto o sistema pode ser sobrecarregado antes de atingir o limite de resistência do material, oferecendo uma medida clara da "folga" do projeto. Quanto maior o valor da MS, maior a margem, o que implica uma maior confiabilidade do componente sob as condições mais extremas. Para o caso em análise temos:
Tabela 5: Margens de segurança
| Número de classe | Margem de segurança |
|---|---|
| 5.8 | 11% |
| 8.8 | 93% |
| 9.8 | 110% |
Fonte: Ana Carolina Carvalho
Com base nos valores apresentados na Tabela 5, optou-se pela utilização de pinos da classe 8.8, pois essa categoria apresenta uma resistência adequada à carga projetada. A classe 9.8 foi descartada por oferecer uma margem de resistência excessiva, suportando 110% a mais do que o necessário, o que resultaria em um superdimensionamento desnecessário. Por outro lado, a classe 5.8 não foi considerada viável, pois sua margem de segurança é reduzida, comprometendo a confiabilidade do sistema. Assim, a escolha pela classe 8.8 justifica-se por proporcionar uma margem de 93% além da carga projetada, garantindo que os pinos desempenhem sua função de travamento de forma segura e eficaz.
Dimensionamento da trava ajustável
Para a fabricação da trava ajustável, será utilizada uma placa de aço carbono com espessura de 0,5 mm, que será usinada para criar os "dentes" responsáveis por definir as inclinações reguláveis. A geometria desses dentes será projetada com base nas distâncias calculadas nessa seção, assegurando que as inclinações sejam precisas e atendam aos requisitos do projeto. Os dentes terão diâmetros específicos, projetados para se encaixarem nos pinos com uma folga mínima. Com essa abordagem, busca-se garantir que a peça tenha um desempenho seguro, permitindo ajustes precisos nas inclinações.
Tabela 6: Distâncias dos dentes da trava
| Caso | Posição do dente com relação ao Ponto C [cm] |
|---|---|
| Posição neutra | 13,5 |
| Posição intermediária | 16,5 |
| Posição máxima | 22,5 |
Fonte: Ana Carolina Carvalho
Dimensionamento do apoio regulável de cabeça
O desenvolvimento do apoio de cabeça ajustável foi realizado com base na norma técnica NBR ISO 7176-7. A norma foi utilizada para determinar as distâncias corporais de referência aplicadas no software Catia, que dispõe de uma funcionalidade específica para análise ergonômica.
No Catia, foram inseridos modelos antropométricos baseados em percentuais da população, com o objetivo de atender à maior diversidade possível de usuários. De acordo com estudos antropométricos, como os apresentados por Kroemer et al., o uso de percentis é uma prática comum para projetar equipamentos ajustáveis que atendam a uma ampla gama de biotipos. Para este projeto, foi definido que o limite mínimo seria o percentil 5 feminino, representando o menor tamanho possível, enquanto o limite máximo seria o percentil 95 masculino, representando o maior tamanho possível. Essa abordagem permite que o dispositivo seja ajustado para atender confortavelmente a 90% da população, excluindo apenas os extremos (menores que o percentil 5 e maiores que o percentil 95).
Definição das alturas mínimas e máximas
Utilizando o módulo Ergonomic Design and Analysis do software CATIA, foram criados manequins digitais representando indivíduos no percentil 5 para mulheres e no percentil 95 para homens. Esses manequins foram cuidadosamente posicionados na cadeira, com o apoio de cabeça ajustado para proporcionar um encaixe ergonômico confortável. Para validar a adequação postural e garantir um design ergonômico eficiente, foi aplicada a ferramenta RULA Analysis, que permite avaliar e classificar o produto com base na postura dos manequins, assegurando uma experiência otimizada em termos de conforto e usabilidade.
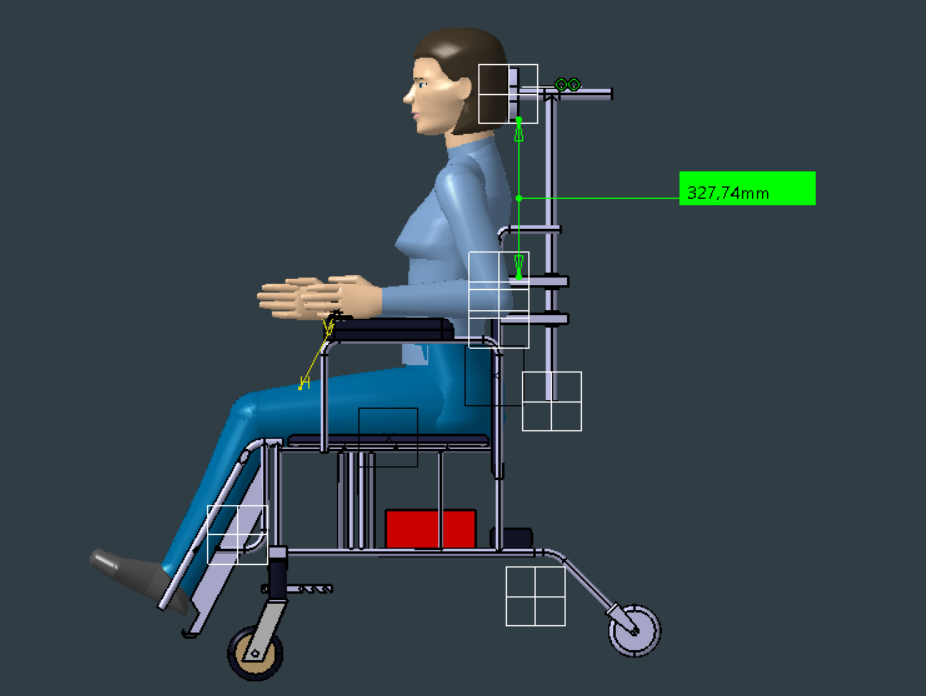
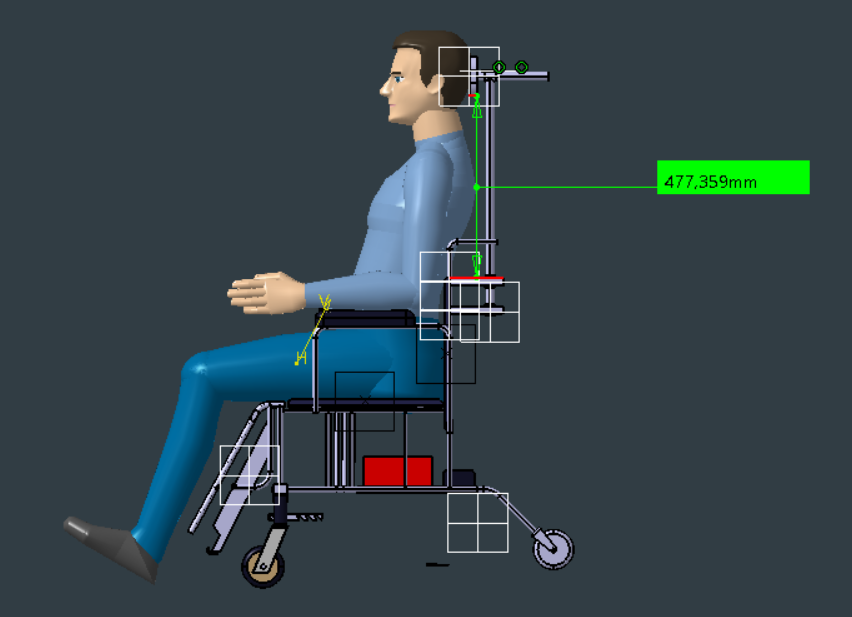
As alturas máximas e mínimas definidas foram 478mm e 328mm, respectivamente.
Definição de materiais para o apoio regulável de cabeça
Em relação aos materiais, a seleção foi orientada por critérios de disponibilidade, custo e demanda estrutural. Foram reaproveitadas barras metálicas disponíveis no laboratório da faculdade. A decisão foi embasada na análise funcional do componente, considerando que o apoio de cabeça não será submetido a cargas significativas ou esforços intensos. Dessa forma, optou-se por materiais de resistência moderada, suficientes para suportar o uso cotidiano, mas que não necessitam de características mecânicas avançadas.
Dimensionamento do dispositivo antitombo traseiro
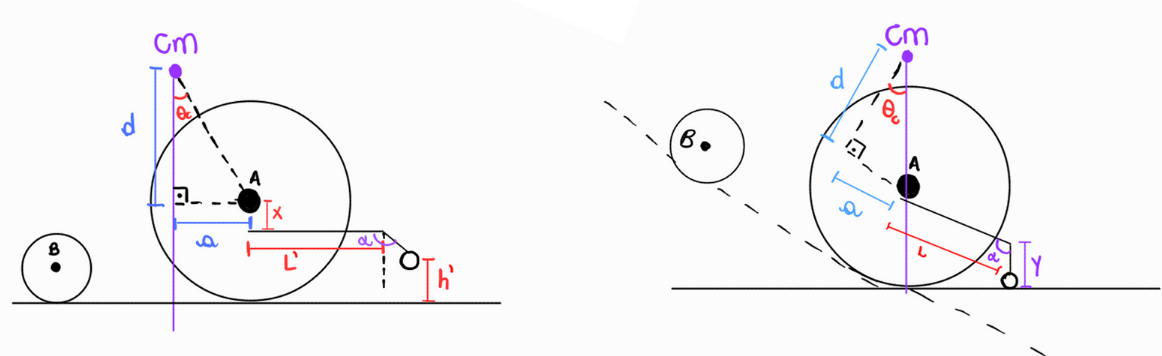
O dispositivo antitombo foi projetado para aumentar a segurança do usuário da cadeira de rodas, prevenindo o tombamento para trás em situações de inclinação acentuada. O conceito baseia-se em um suporte que entra em contato com o solo no momento exato em que o centro de massa da cadeira ultrapassa o eixo da roda traseira, caracterizando o ponto crítico de instabilidade, como ilustrado na figura abaixo.
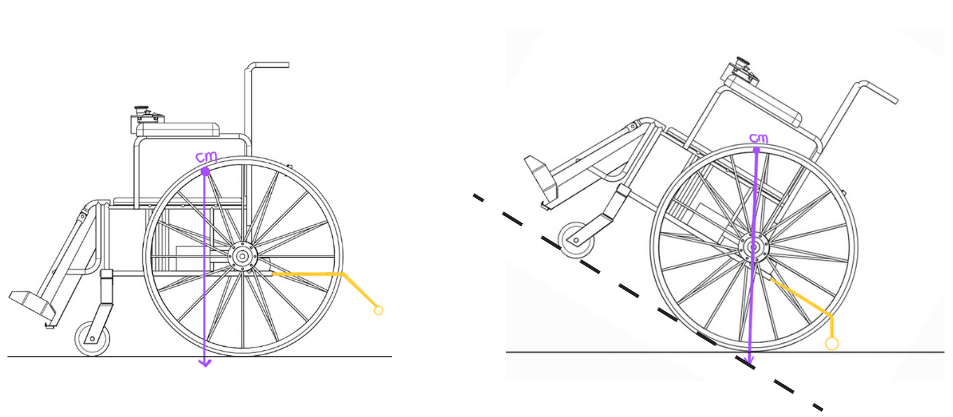
O esquema do problema, juntamente com as variáveis de interesse, está apresentado na figura abaixo.
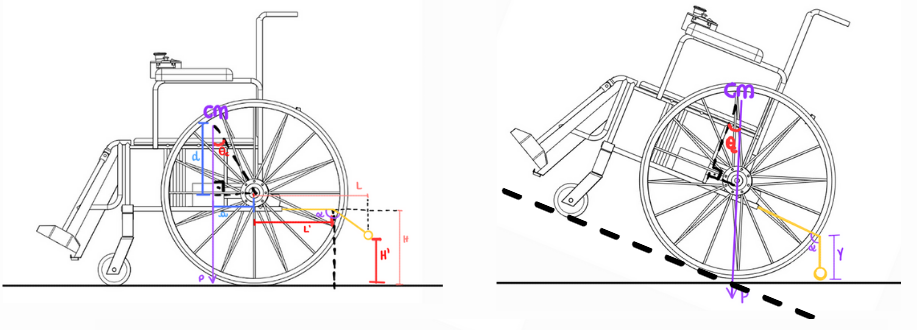
Definição dos parâmetros utilizados
Os cálculos foram realizados com base nos seguintes parâmetros, com as referências já mencionadas anteriormente.
- Raio da roda principal (Ra): 0,3 m.
- Distancia horizontal da roda A ate o cm (a):0,151656m
- Distancia vertical da roda A ate o cm (d):0,256757m
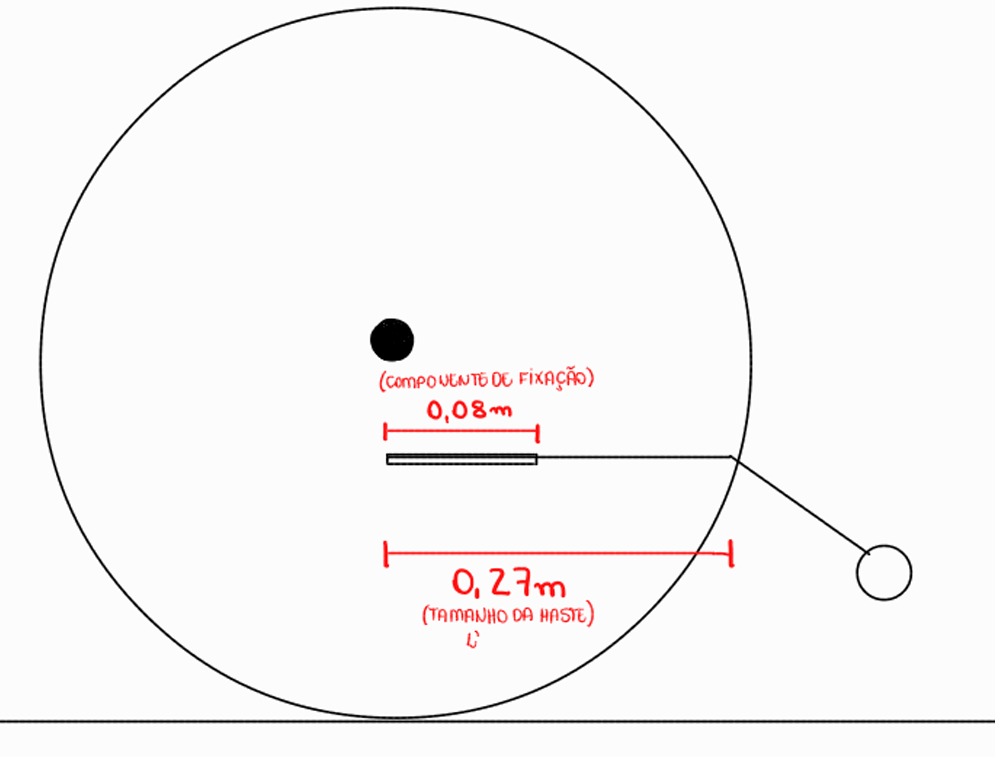
- Distância da haste até o eixo da roda (L'): 0,27 m
A haste do dispositivo antitombo será fixada em um componente já existente de fábrica na cadeira, cuja altura em relação ao chão é conhecida, assim como a distância até o final da roda. O dispositivo foi projetado de forma que o comprimento da haste, até o ponto em que ocorre a dobra para a rodinha, seja equivalente à distância do eixo da roda até a borda da roda, considerando a altura de fixação disponível. Essa abordagem foi adotada para garantir que o comprimento da haste (L') corresponda exatamente à extensão necessária para alcançar o final da roda, assegurando um alinhamento adequado.
Etapas do Cálculo
Passo 1: Determinação do ângulo crítico de tombamento (Tetac)
O ângulo crítico foi calculado utilizando a relação trigonométrica entre a altura e a distância horizontal do centro de massa:
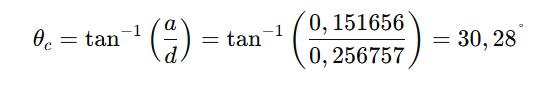
O ângulo crítico de tombamento encontrado foi de 30,28°, o que significa que, ao inclinar a cadeira de rodas até esse ângulo, a rodinha antitombo deve estar em contato com o chão.
Passo 2: Cenário de dimensionamento simplificado
A estratégia adotada consistiu em considerar um cenário simplificado, no qual a haste da rodinha é reta (𝛼=180°) e a rodinha toca diretamente o chão. Essa abordagem foi definida previamente com o objetivo de determinar o comprimento máximo da haste da rodinha, incluindo o seu tamanho quando inclinada em um ângulo 𝛼.
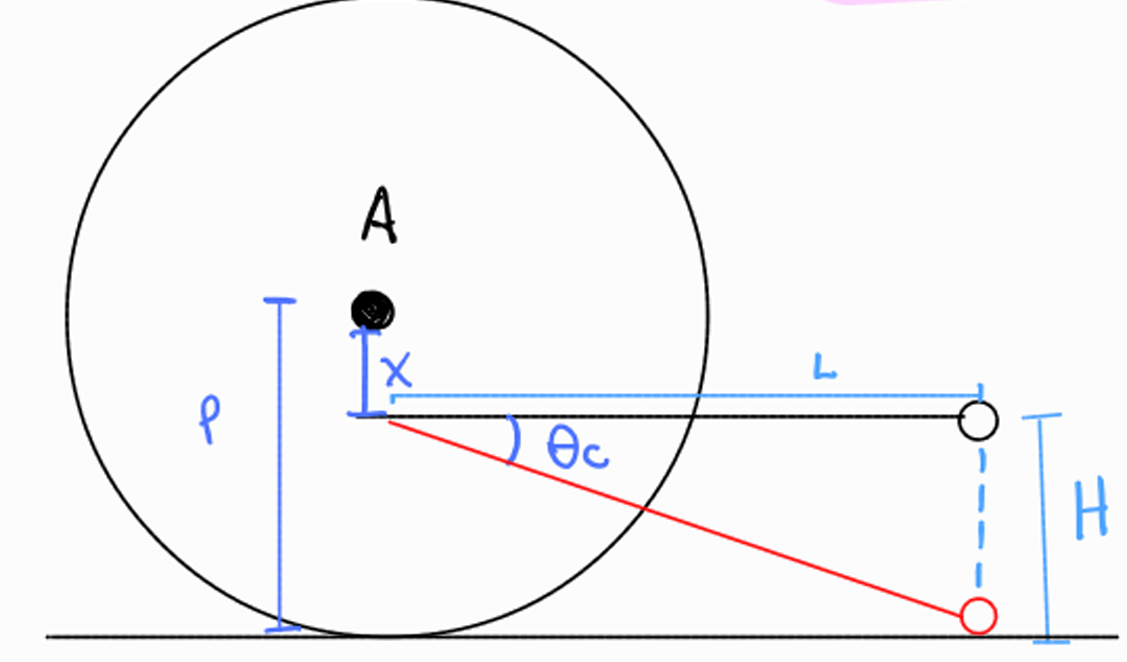
Observa-se que o valor de 𝐻 corresponde à diferença entre a altura 𝑃 (raio da roda) e a distância 𝑥, que representa a posição do ponto de fixação em relação ao eixo da roda. Dessa forma, parte-se para o calculo de L, a partir de definições geometricas.
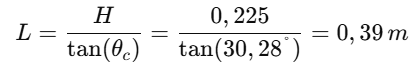
Passo 3: Determinação de alpha
Agora que os valores de H e L foram determinados a partir do cenário simplificado, é possível definir o ângulo 𝛼, que corresponde à curvatura da haste a 0,27 m para a instalação da rodinha. Esse ângulo foi estabelecido com base em uma premissa definida pelo grupo de estruturas, visando garantir que, ao atingir o ângulo crítico de tombamento, a rodinha e a haste inclinada formem um ângulo de 90° com o chão, permanecendo na posição vertical e permitindo que o impacto ocorra de forma vertical. O esquema com os angulos pode ser visualizado na imagem abaixo.
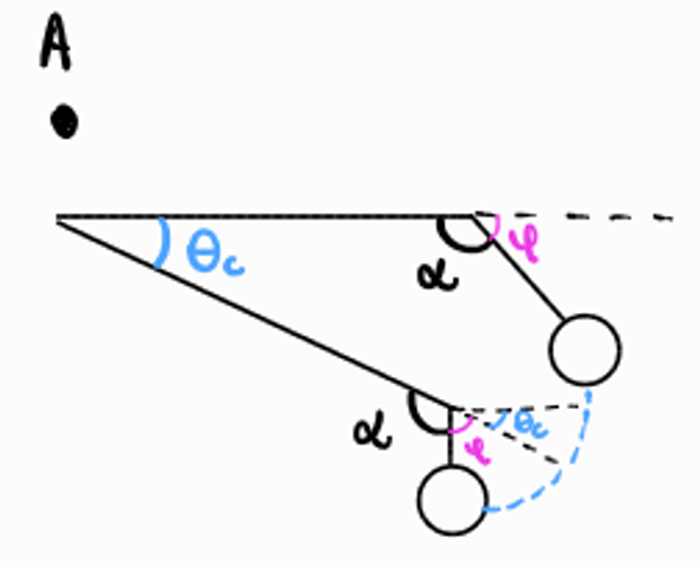
O cálculo por definições trigonométricas fica da sequinte forma:
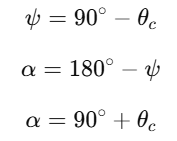
Com os valores substituidos encontra-se:
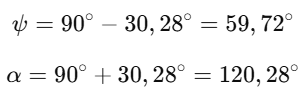
Portanto, o ângulo que a haste do dispositivo terá é 𝛼 = 120,28°.
Passo 3: Determinação do comprimento da haste inclinada e da altura da rodinha
Uma vez que o caso simplificado é conhecido e temos os valores de 𝐿 e 𝐻, e o ângulo 𝛼 já foi calculado, pode-se determinar o comprimento da haste que estará inclinada em 𝛼 e a altura da rodinha em relação ao solo quando a cadeira está em sua condição normal (sem inclinação).
Primeiramente, como se sabe o valor de 𝐿 e 𝐿′, obtém-se o valor de 𝑦, que é dado por:
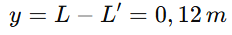
Dessa forma, o comprimento da haste inclinada é de 0,12 m. A partir desse valor, foi feito um equacionamento considerando o triângulo formado pelos pontos finais da haste do caso simplificado e o ponto final da haste inclinada. Observa-se que o ângulo que a haste inclinada faz com a projeção da haste do caso simplificado é 𝜓.
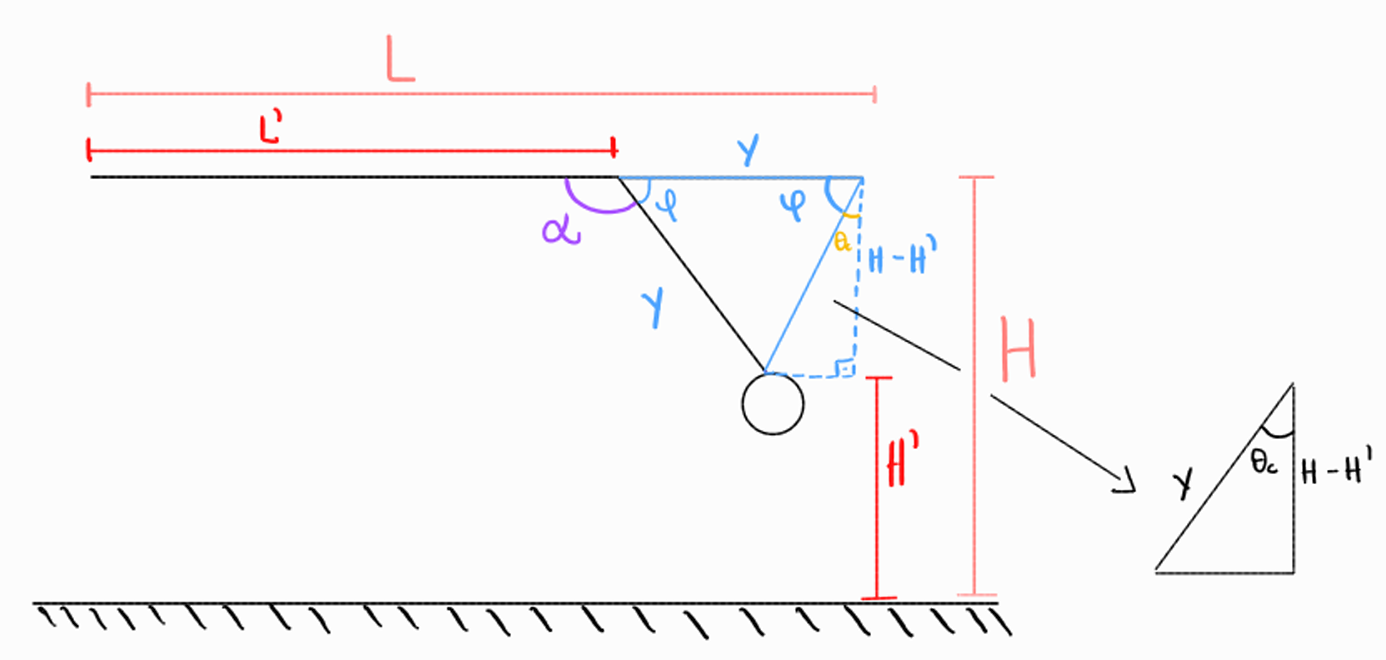
Aproximando o triângulo para um triângulo equilátero (devido ao ângulo 𝜓 ser muito proximo de 60°, as diferenças são desprezíveis e essa aproximação pode ser aplicada), é possível estabelecer um equacionamento com base na semelhança de ângulos e em relações de trigonometria para encontrar o valor de 𝐻' (distância da rodinha até o chão).
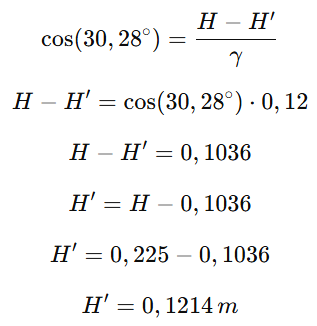
Conclusão
Após todo o equacionamento necessário, o dispositivo antitombo pôde ser devidamente dimensionado, considerando as condições geométricas, o ângulo crítico de tombamento e as relações trigonométricas aplicadas. O comprimento da haste inclinada e a altura da rodinha em relação ao solo foram determinados de forma a garantir a eficácia do dispositivo, proporcionando maior estabilidade e segurança à cadeira de rodas.
O resultado final do dimensionamento do dispositivo antitombo pode ser visualizado na imagem abaixo.
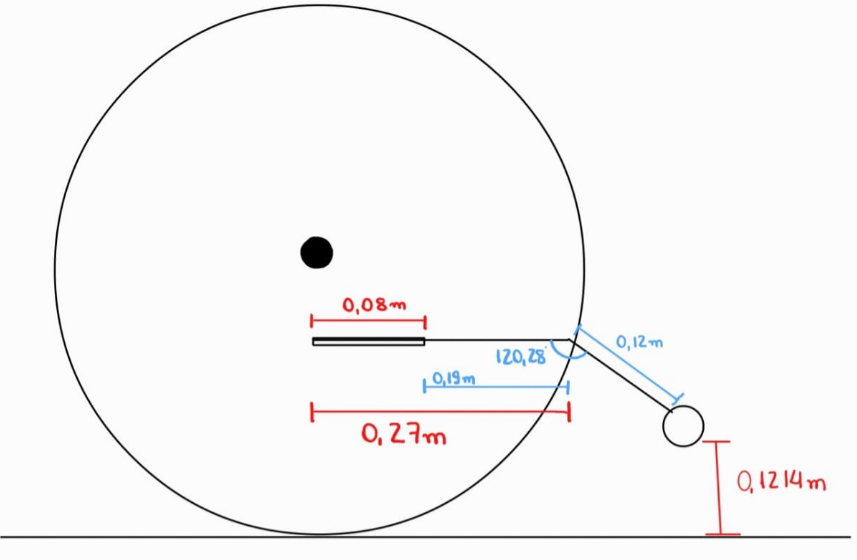
Adicionalmente ao dimensionamento geométrico realizado de forma analítica, foram selecionados os materiais adequados e o dispositivo antitombo foi desenvolvido. Para agregar mais confiabilidade ao dimensionamento e à escolha dos materiais, foi realizada uma simulação no ANSYS, cujos resultados podem ser visualizados no capítulo de cálculos numéricos.
Referências
-
ABNT. NBR ISO 7176-7:2008. Cadeiras de rodas - Parte 7: Medição de dimensões de assentos e rodas. Rio de Janeiro: Associação Brasileira de Normas Técnicas, 2008. Acesso em: 18 dez. 2024.
-
ABNT. NBR ISO 7176-13:2009. Cadeiras de rodas - Determinação do coeficiente de atrito de superfícies de ensaio. Rio de Janeiro: Associação Brasileira de Normas Técnicas, 2009. Acesso em: 18 dez. 2024.
-
HIBBELER, R.C. Estática: Mecânica para Engenharia. 13. ed. São Paulo: Pearson Education, 2016. Acesso em: 18 dez. 2024.
-
ABNT. NBR ISO 7176-3:2015. Cadeiras de rodas - Determinação da eficácia dos freios. Rio de Janeiro: Associação Brasileira de Normas Técnicas, 2015. Acesso em: 18 dez. 2024.
-
SHIGLEY, J.E. Elementos de Máquinas. 9. ed. São Paulo: McGraw-Hill, 2011. Acesso em: 18 dez. 2024.
-
PASCHOARELLI, L. C.; MENEZES, M. S., orgs. Design e ergonomia: aspectos tecnológicos [online]. São Paulo: Editora UNESP; Cultura Acadêmica, 2009. 279 p. ISBN 978-857983-001-3. Disponível em: http://books.scielo.org. Acesso em: 09 jan. 2024.
-
HUET, M.; MORAES, A. Medida de pressão sobre a pelve na postura sentada em pesquisas de ergonomia. Fisioterapia Brasil, v. 4, n. 6, p. 438-444, nov./dez. 2003. Disponível em: https://www.researchgate.net/publication/338962821_Medidas_de_pressao_sob_a_pelve_na_postura_sentada_em_pesquisas_de_ergonomia. Acesso em: 18 dez. 2024.
-
MSD MANUAL. Hipotensão ortostática. MSD Manual Professional Edition. 2024. Disponível em: https://www.msdmanuals.com/pt/profissional/doen%C3%A7as-cardiovasculares/sintomas-de-doen%C3%A7as-cardiovasculares/hipotens%C3%A3o-ortost%C3%A1tica. Acesso em: 18 dez. 2024.
-
BALL, K. M. Tilt and recline: understanding all the angles. Directions Magazine, 2017. Disponível em: https://nrrts.org/wp-content/uploads/2019/06/DIRECTIONS-2017.2_CEU-clinical-perspective.pdf. Acesso em: 18 dez. 2024.
-
ABNT. NBR ISO 7176-11: Cadeiras de rodas – Parte 11: Bonecos de Ensaio. Associação Brasileira de Normas Técnicas, 2009. Acesso em: 18 dez. 2024.
-
BEER, F. P.; JOHNSTON Jr., E. R.; DEWOLF, J. T.; MAZUREK, D. F. Resistência dos materiais. 6. ed. Porto Alegre: AMGH Editora, 2017. Acesso em: 30 nov. 2024.
-
ISO 898-1: 2013. Mechanical properties of fasteners made of carbon steel and alloy steel – Part 1: Bolts, screws and studs. Geneva: International Organization for Standardization, 2013. Acesso em: 9 jan. 2025.
-
NORTON, R. L. Projeto de máquinas: uma abordagem integrada. Tradução técnica de João Batista de Aguiar, José Manoel de Aguiar [et al.]. 2. ed. Porto Alegre: Bookman, 2004. 931 p.
-
KROEMER, K. H. E.; KROEMER, H. B.; KROEMER-ELBERT, K. E. Ergonomics: How to Design for Ease and Efficiency. 3. ed. New York: Wiley, 2019. Acesso em: 15 jan. 2025.
Tabela de versionamento
| Versão | Data | Descrição | Responsável |
|---|---|---|---|
| 1.0 | 30/11/2024 | Cálculo do torque requerido do motor | Júlia Laryssa Messias |
| 2.0 | 30/11/2024 | Mecanismo móvel para apoio de pernas | Ana Carolina Carvalho |
| 3.0 | 01/12/2024 | Revisão do artefato | Ana Carolina Carvalho |
| 4.0 | 20/12/2024 | Atualização e melhoria do mecanismo móvel para apoio de pernas | Ana Carolina Carvalho |
| 5.0 | 21/12/2024 | Atualização e melhoria do cálculo do torque requerido do motor | Júlia Laryssa Messias |
| 6.0 | 09/01/2025 | Atualização e melhoria do mecanismo móvel para apoio de pernas | Ana Carolina Carvalho |
| 7.0 | 20/01/2025 | Atualização e melhoria do cálculo do torque requerido do motor | Júlia Laryssa Messias |
| 8.0 | 20/01/2025 | Dimensionamento do apoio regulável de cabeça | Maria Eduarda Lourenção |
| 9.0 | 29/01/2025 | Atualização e melhoria do mecanismo móvel para apoio de pernas com base no protótipo | Ana Carolina Carvalho |
| 10.0 | 31/01/2025 | Dimensionamento do dispositivo antitombo | Júlia Laryssa Messias |
| 11.0 | 18/02/2025 | Atualização e melhoria do apoio regulável de cabeça | Maria Eduarda Lourenção |